Image Analysis
In this tutorial, we will analyze an image thanks to its stars. What does FWHM mean? Why is it a good measure of the quality of your picture?
Dynamic PSF tool #
Dynamic PSF has been present for quite a while in Siril. It can very be useful in many occasions, like global star registration. But a vast majority of users do not know how to use it.
Dynamic PSF window when star detection has been activated.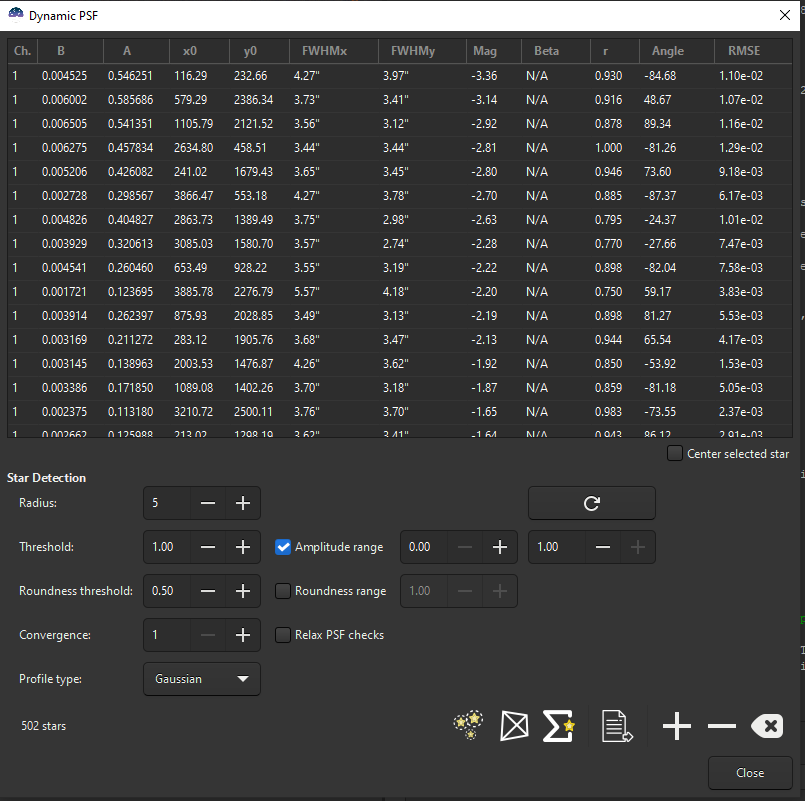
Image Information and Dynamic PSF.
A bit of theory #
Point Spread Function, a.k.a. PSF , is a mathematical function that describes the response of an imaging system to a point source. In theory, stars being far far away from us, they could be considered as perfect point sources. Well, in theory. In practice, their photons will interact with different media before reaching us: the Earth atmosphere, the glass of our refractors (or the mirror of our reflectors) and the camera sensors. All these interactions will tend to spread the initial source point, hence the name of the function. To keep it simple, if you are imaging with a high-end optics under a Chile-like atmosphere, the stars will look pin-point sharp. On the contrary, imaging with a toyscope just above the horizon will end up with large fuzzy stars.
Modelling the PSF #
In Siril, the PSF is approximated by “profil”. You can choose either a Gaussian profil or a Moffat profil. Once the fitting is done, it returns important parameters like FWHM, roundness, magnitude, etc…
- Ch: Channel where the PSF was applied.
- B: Average of local background.
- A: Amplitude of the fitted PSF (maximum value).
- (x0, y0): Centroid coordinates in pixel units.
- (FWHMx, FWHMy): The FWHM on the X and Y axis in PSF coordinates.
- Mag: Relative magnitude of the star.
- r: Roundness of the star, r=1 means a perfect round star.
- Angle: Rotation angle of the X axis of PSF coordinates in degrees.
- RMSE: Root-Mean-Square Error of the fit.
FWHM as a selection criterion #
The figure below shows a 1-D gaussian curve. Its FWHM (Full Width at Half Maximum) represents the width of the curve when the value is at half its maximum.
Full Width at Half Maximum (FWHM).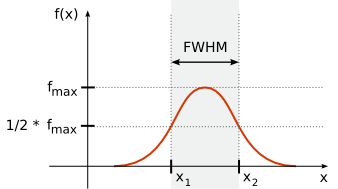
Roundness as another criterion #
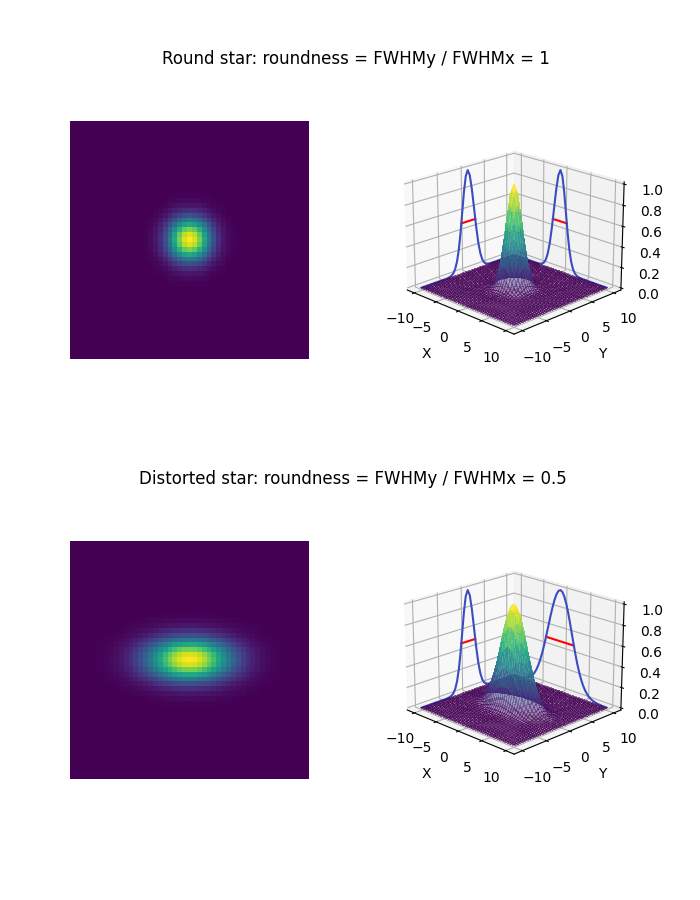
The roundness of a star is defined as the ratio between its FWHM along y-axis and x-axis. A roundness of 1 describes a perfectly round-shaped star while a roundness of 0.5 defines a star twice as large along x-axis than along y-axis. It is therefore an additional measure which, associated to FWHM (filters can be applied on both values at stacking stage), enables to narrow down the selection of your sharpest images.
Using Dynamic PSF tool #
There are two ways to use this tool in Siril.
- One star at a time, selecting them with care. Select an area around a star then right click and select
Pick a star. This will add the star to the Dynamic PSF tool. The main advantage is that each star added to the tool has been chosen by the user.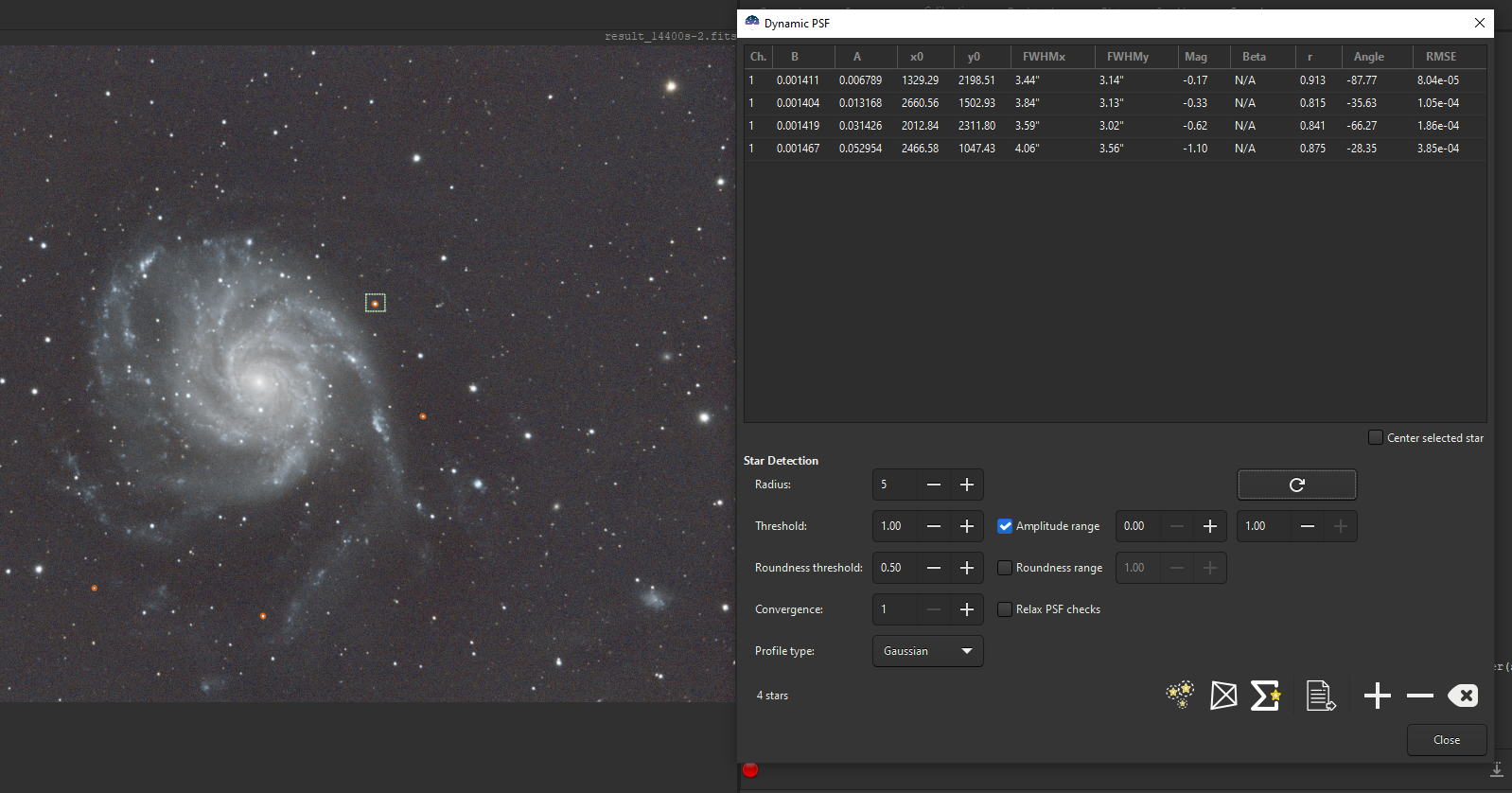
Manual selection can provide better results as the number and which stars are selected is controlled by the user.
- Globally, by clicking on the star detection button. Siril will automatically detect anything that looks like a star. Frequently, the algorithm will detect bright objects as false positive, as can be seen in the figure below. While this has not impact of the registration process, the result of the analysis will be of lesser quality. Adjusting the detection threshold (increasing it in that case) will give better results.
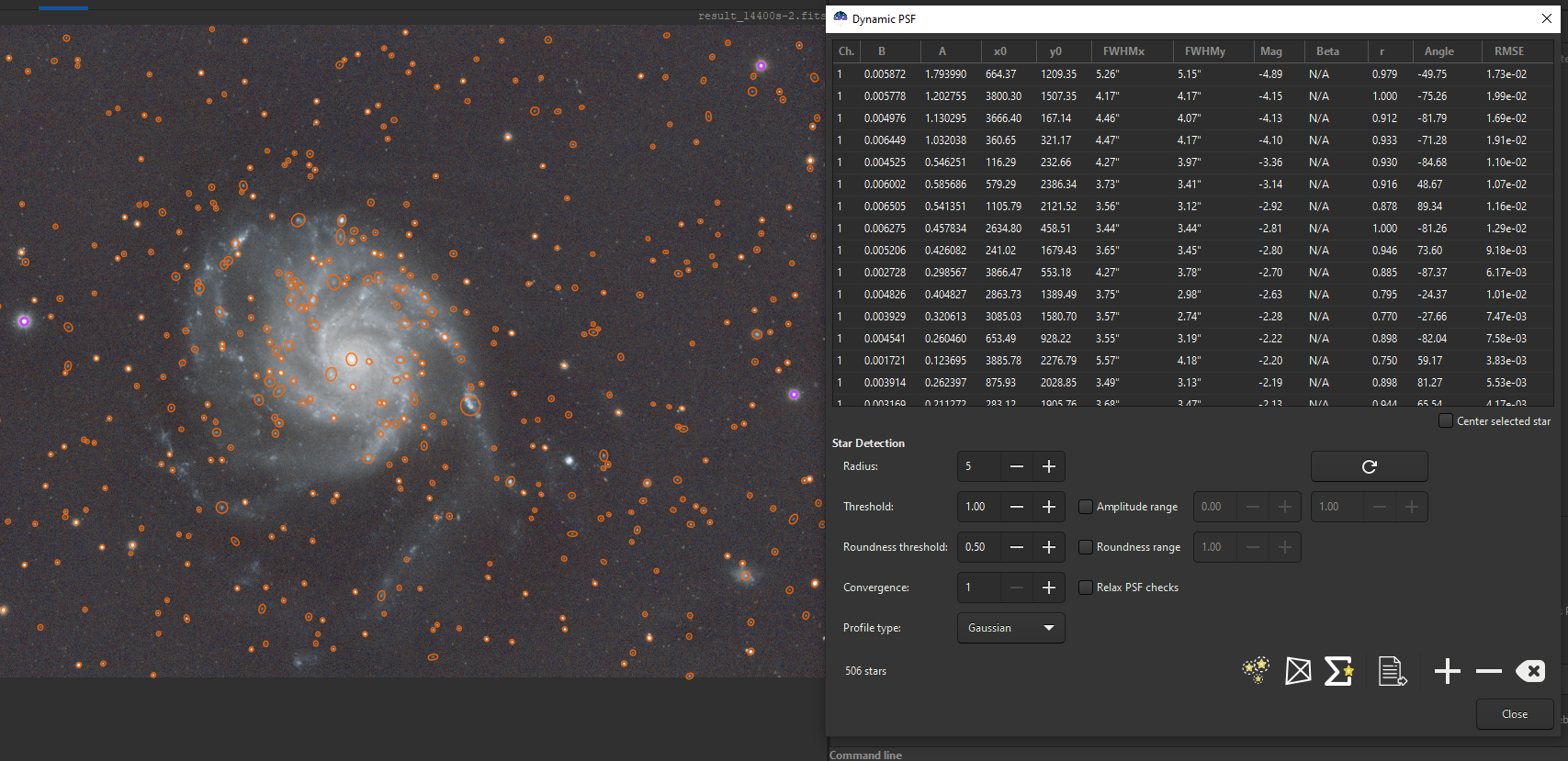
Global star detection as done by the star registration algorithm. For the sake of keeping the calculations quick, the gaussian function fitting does not account for the angle of the function, contrarily to when it is done one star at a time. This has very little impact on the final result.
With a closer look, one can see that:
- The detected stars are surrounded by an orange ellipse, whose elongation is related to the roundness of the star.
- If a star is sourrounded by a violet shape, it means it has been detected as a saturated star.

Instead of computing the whole stars PSF, it is also possible to limit the amount of stars to consider with 2 criteria:
- the max amplitude, A. The default value is in the range [0,1] (normalized pixel value), but the
Amplitude rangecan be adjusted. - the max roundness, r. The default value is 1.0, but the
Roundness rangecan also be adjusted. This tends to limit the computation time in the case of a particularly populated field of view.
Once all the stars have been loaded in the window, you can sort them by any parameter, in increasing or decreasing order. You can also export this list in csv format by clicking on the appropriate button in the toolbar.
If you wish to clear the whole list of stars, just type the command clearstar in the command line.
One interesting point: if you click on a star in the list, it will be automatically pointed in the image with blue axes, to ease locating it. And inversly, if you pick an already detected star in the image, this star will be highlighted in the list.
Finally, and it is one of the main merits of the tool, you can get average values of the parameters for all the stars selected in the image.
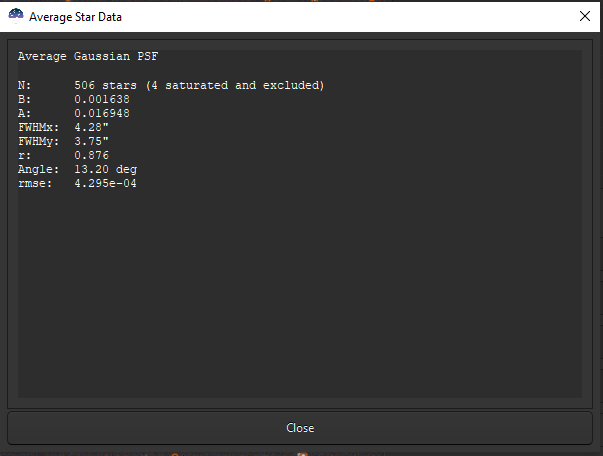
Use case #
When global registration fails, this tool can be very helpful to understand why and fix star detection. Head to the Dynamic PSF window and play with the detection parameters like threshold and roundness. After each change, don’t forget to check the effect by clicking again on the detection button.

Here is a particular example of an image where the default parameters do not allow a global registration: only one star is detected. However, it is easy to see in autostretch mode that several stars are present in the image, and even in sufficient number to allow registration.
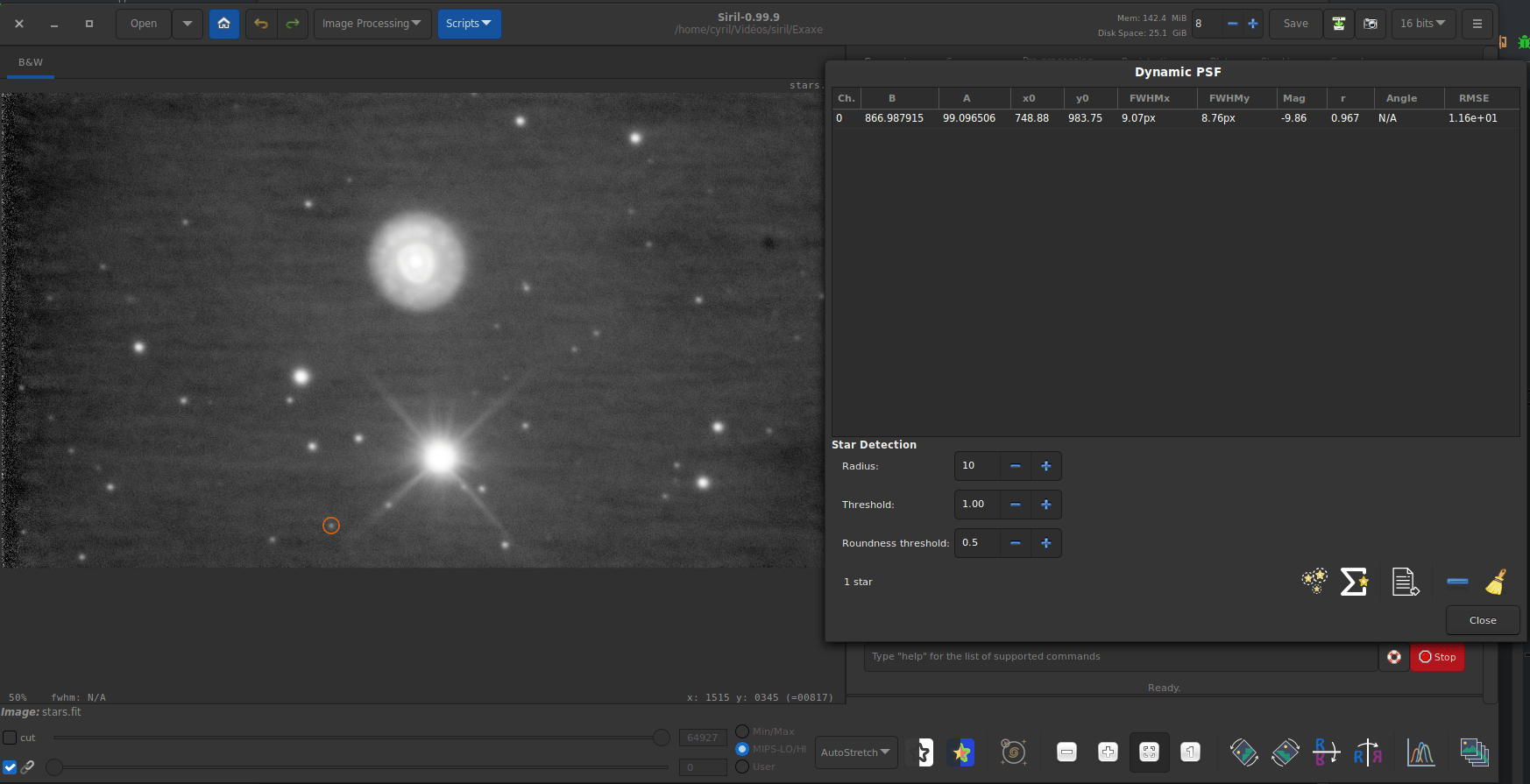
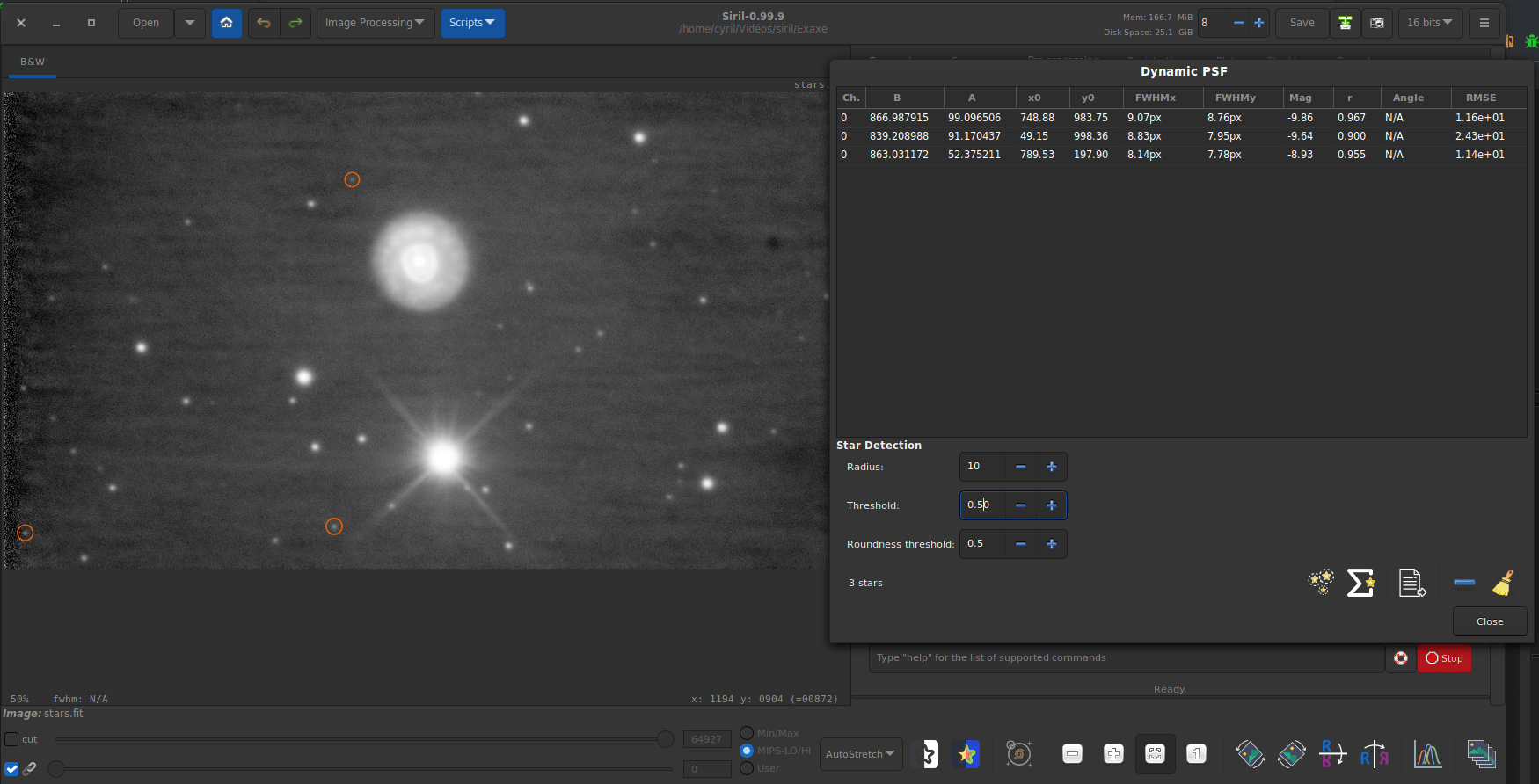
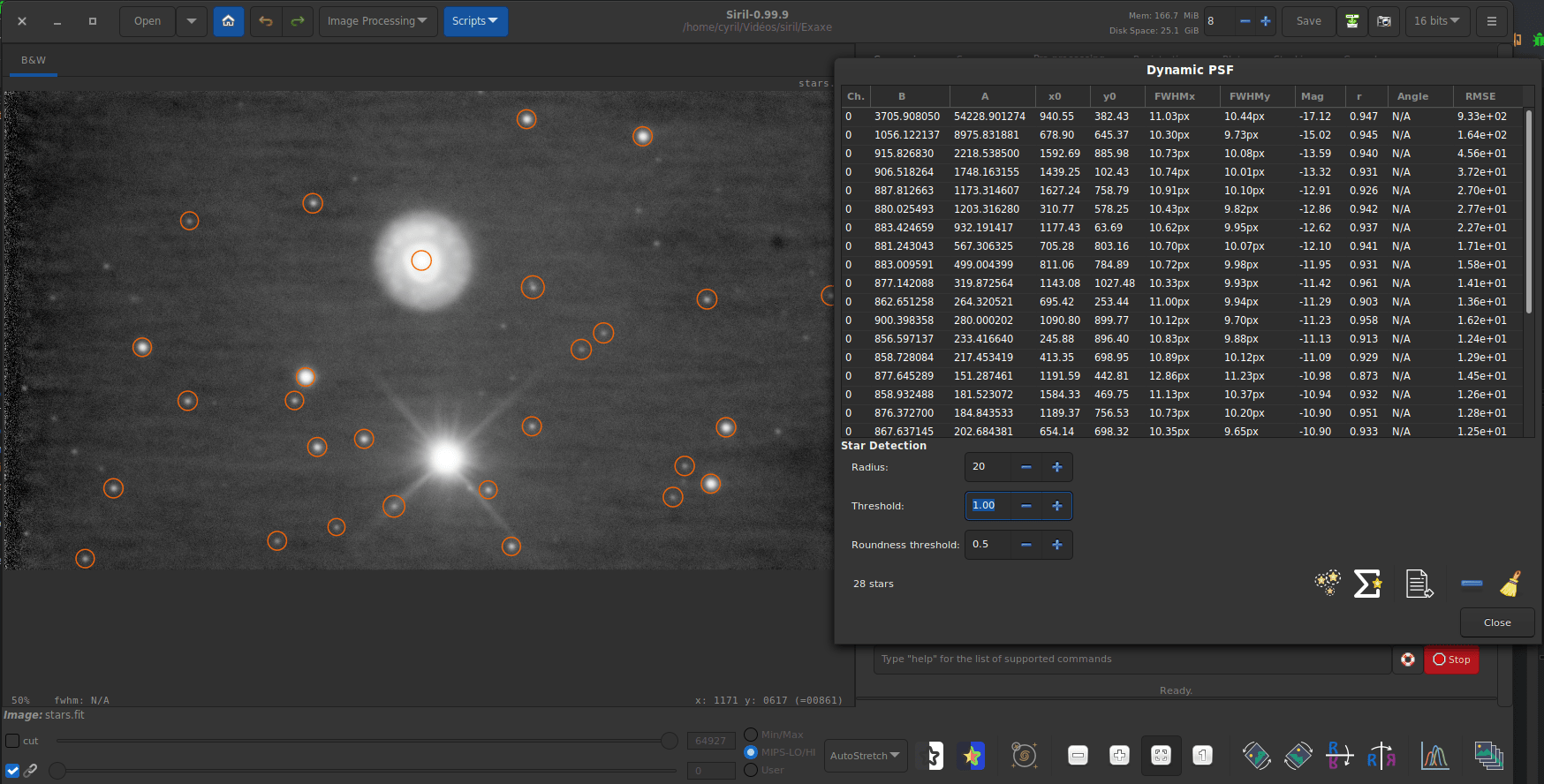
Of course, it is also possible to tune the additionnal parameters such as the Convergence or the Profile type (Moffat vs gaussien).