Offsets synthétiques
Dans ce tutoriel nous verrons comment utiliser des biais synthétiques pour calibrer les flats et comment déterminer leur niveau. J’utiliserai les termes biais ou offset indifféremment.
Pourquoi (et quand) puis-je utiliser un offset synthétique ? #
L’objectif principal de soustraire un offset maitre des flats est de définir leur valeur zéro de sorte que lors de la division des brutes corrigées par le dark maitre, leurs courbures correspondent, comme expliqué en annexe . Il ne s’agit pas d’essayer de supprimer le bruit de lecture (soustraire une image maître ne supprime jamais le bruit, cela supprime un signal tout en ajoutant du bruit). Et dans le cas particulier des flats, il ne s’agit pas non plus de supprimer d’autres variations de niveau, sauf si votre capteur a :
- un ampglow important et vous exposez vos flats pendant une durée significative (quelques secondes ou plus).
- pas de régulation thermique et vous travaillez sous des températures élevées, donc éventuellement un courant de dark important qui rendra le niveau zéro dépendant à la fois de la température et du temps.
Les petites variations, lignes ou quadrillage, que vous avez pu observer sur votre offset maitre en mode d’affichage Histogramme existent, comme on peut le voir dans l’illustration suivante.
En mode d’affichage Égalisation d’histogramme, un motif est clairement visible. Cependant, les statistiques montrent que ces variations sont assez faibles et ne jouent pas un grand rôle par rapport à la lumière enregistrée dans une image flat.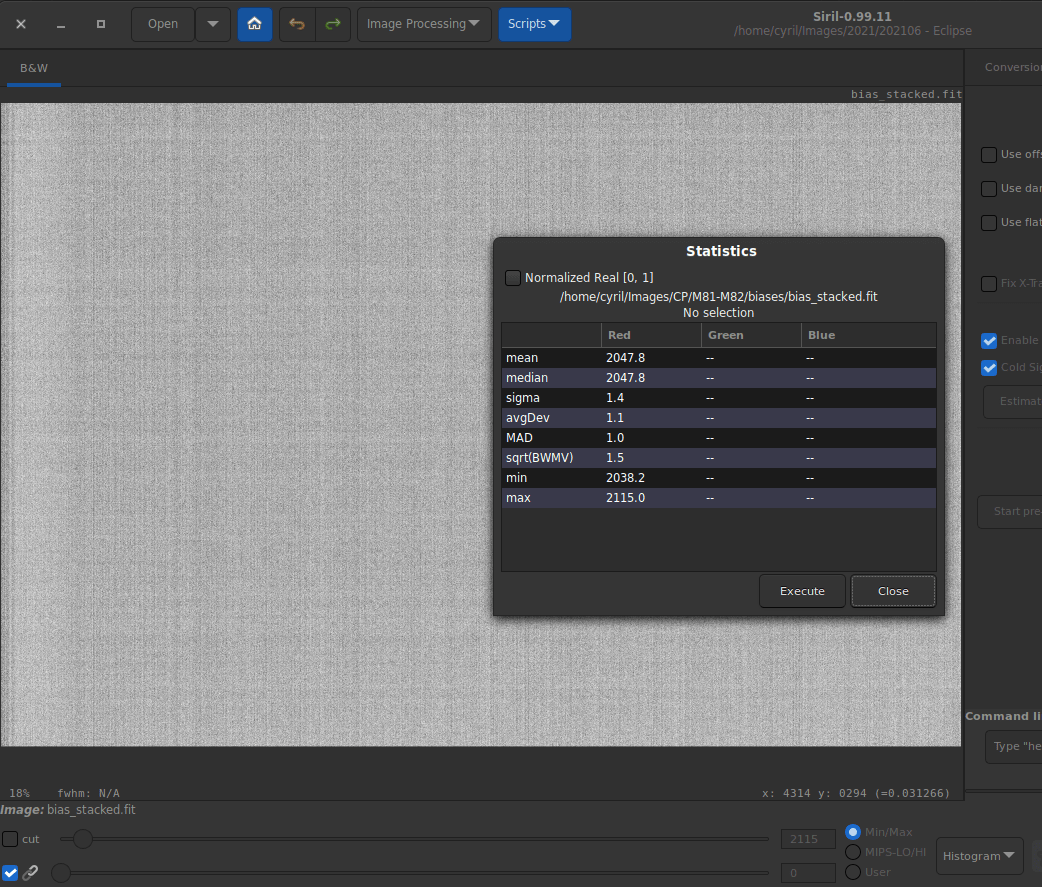
Mais ils sont si petits par rapport à la quantité et à la variabilité du nombre de photons reçus lors de l’exposition d’un flat qu’ils n’ont pas vraiment d’importance. Pour vous en convaincre, rappelez-vous simplement que vous ne supprimez jamais un offset maitre des images que vous prenez à la lumière du jour, simplement parce qu’il y a suffisamment de signal et de dynamique. Ceci n’est bien sûr pas valable pour les images brutes du ciel profond qui ont un signal très faible.
Ainsi, au lieu de soustraire un offset maitre qui ajouterait intrinsèquement du bruit, le principe d’utiliser un offset synthétique est de simplement soustraire un niveau en ADU de vos flats avant de les empiler.
Déterminez le niveau d’offset avec une caméra astronomique #
Avec une caméra, l’offset est un paramètre qui peut être défini par l’utilisateur. La valeur que vous définissez dans votre logiciel d’imagerie n’est cependant pas le niveau effectif en ADU que vous pourriez mesurer dans vos biais. Afin de déterminer la relation entre le paramètre de réglage et le niveau ADU, vous pouvez suivre cette procédure simple. Je vous recommande de le faire même si vous ne modifiez jamais ce paramètre, pour déterminer le multiplicateur avec plus de précision.
- prenez une série de biais, une seule par valeur de réglage. Dans l’exemple ci-dessous, avec ma ZWO 294MC, j’ai utilisé des paramètres d’offset entre 10 et 50 par pas de 10, donc 5 images au total. Les valeurs possibles sont comprises dans la plage $[0,100]$, mais cela est spécifique à chaque modèle. Ne jamais utiliser un offset de 0 car les statistiques seront biaisées par un clipping au zéro (c’est exactement pour éviter cela que les fabricants de caméras ajoutent une tension d’offset).
- Ouvrez Siril et définissez le répertoire où vos photos sont stockées comme répertoire de travail.
- Convertissez en séquence en tapant
convert offsetdans la ligne de commande. - Extrayez les statistiques de la séquence en tapant
seqstat offset offset.csv basicdans la ligne de commande. Cela calculera les statistiques pour toutes les images de la séquence et les enregistrera dans le fichier offset.csv. - Ouvrez le fichier csv sous forme de feuille de calcul (les valeurs sont séparées par des tabulations). Si vous obtenez des valeurs de statistiques sous forme de flottants, et non d’ADU – cela dépend de votre préférence de profondeur de bit dans Siril – elles peuvent être converties en ADU en multipliant par 65535 $(=2^{16}-1)$. J’ai choisi de tracer la médiane comme estimateur de localisation, plus robuste aux valeurs aberrantes (pixels froids/chauds) que la moyenne. Et je la trace en fonction des valeurs d’offset que j’ai entrées pour chaque image. Si j’ajoute une tendance linéaire, forçant l’ordonnée à l’origine à 0, j’obtiens ceci:
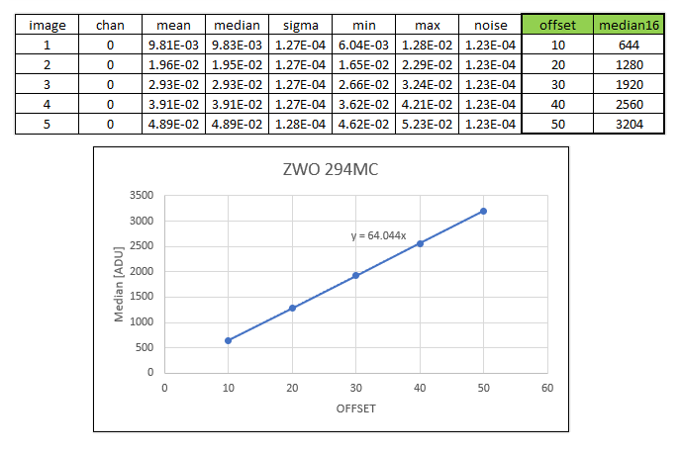
Niveau d’ADU en fonction de l’offset pour une caméra ZWO 294MC
- Nous pouvons voir que le niveau médian de mes biais varie linéairement avec la valeur de réglage par un facteur de 64, de sorte que
OffsetLevel [ADU] = 64 * OFFSET. Dois-je conserver les chiffres après la virgule? Non, nous recherchons une valeur entière. Plus précisément, nous recherchons une valeur de multiplicateur qui est un multiple de 4 pour cette caméra particulière, qui dispose d’un ADC (Analog Digital Convertor) 14 bits. De telle sorte qu’il y a au moins un facteur 4 $(=2^{16-14})$ entre la sortie du convertisseur et la profondeur de bit de mon fichier FITS (16b). De même, une caméra 12b devrait avoir un multiplicateur qui est un facteur de 16 $(=2^{16-12})$, tandis que pour une caméra 16b, il n’y a aucun moyen de le savoir à l’avance. Par exemple, pour une ZWO 2600MC, le multiplicateur est de 10.
Déterminez le niveau d’offset avec un reflex numérique #
Même si un reflex numérique est plus susceptible d’être affecté par la sensibilité au courant dark, vous pouvez toujours essayer la même méthode. Avec un reflex numérique, on ne peut pas spécifier une valeur d’offset. Toujours est-il que dans les coulisses, le fabricant le définit automatiquement avec le réglage ISO. J’ai répété la même procédure avec mon Canon 700D, pris une série de biais en faisant varier les ISO, extrait les statistiques et tracé le niveau médian en fonction de l’ISO. J’obtiens la courbe ci-dessous :
Niveau d’ADU en fonction de l’ISO pour un Canon 700D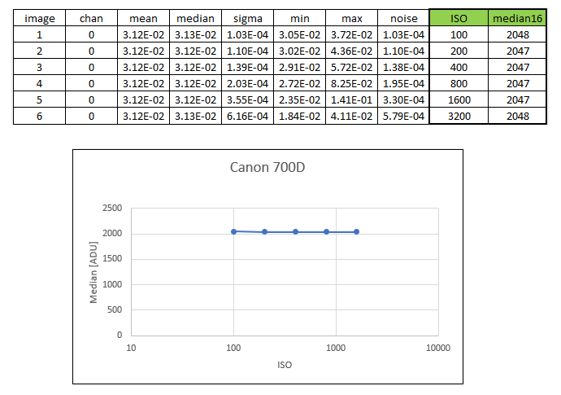
2048, ce qui est assez standard, les fabricants faisant souvent le choix d’utiliser une puissance de 2. Il se pourrait que pour d’autres modèles, l’indépendance à l’ISO ou la valeur en puissance de 2 ne soient pas vraies, donc vous devez vérifier avec votre propre matériel.
Et maintenant? #
Maintenant que vous avez déterminé le niveau de vos biais en ADU en fonction du réglage de votre capteur, comment traiter vos flats avec ces informations?
Si vous traitez manuellement :
Lors de la calibration de vos flats, au lieu de spécifier le chemin d’un offset maitre, vous pouvez saisir directement des expressions dans le sélecteur de dossier telles que :
=2048=64*$OFFSET
Les signes = et $ sont obligatoires pour que cela fonctionne. Le niveau doit être donné en ADU (pas en flottant, même si vous travaillez en 32b).

Si vous traitez avec des commandes ou des scripts :
La commande calibrate accepte maintenant de passer une expression pour l’option -bias= :
calibrate flat -bias="=256"calibrate flat -bias="=10*$OFFSET"
Le =, $ ainsi que les guillemets autour de l’expression sont obligatoires pour que cela fonctionne. La deuxième expression nécessite également que votre logiciel d’imagerie écrive une clé OFFSET ou BLKLEVEL dans les en-têtes FITS. Le niveau doit être donné en ADU (pas en flottant, même si vous travaillez en 32b).
Annexe: Comprendre comment les flats corrigent les brutes #
Le but de cette section est de donner un peu plus de détails sur la façon dont les différents niveaux jouent un rôle dans la correction des brutes par les flats. Nous ne tiendrons pas compte ici de considérations sur le bruit (encore une fois, le bruit ne disparaît pas par soustraction ou par division d’une image maitre, il diminue en faisant la moyenne sur de nombreuses réalisations du même processus aléatoire). Nous ignorerons également les variations spatiales particulières tels que l’ampglow ou les poussières.
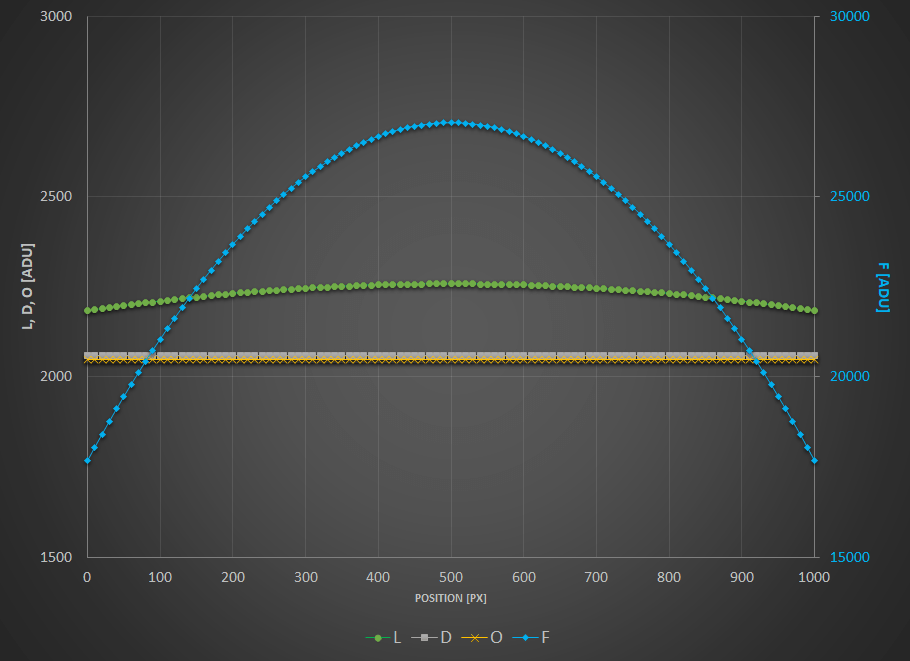
Si nous essayons de quantifier l’intensité des pixels de fond dans les différentes images, nous pouvons écrire les expressions suivantes :
Pour les brutes $L$, nous avons une composante spatiale d’illumination, $a - b(x-\frac{W}{2})^2$. Nous avons choisi ici une variation quadratique avec une valeur maximale $a$ au milieu de l’image de largeur $W$, paire autour du centre du capteur. Ce n’est pas la forme spatiale exacte du vignettage, mais c’est une assez bonne approximation pour comprendre comment cela fonctionne. En plus de ce terme spatial, il existe un terme variant avec le temps d’exposition qui est généralement appelé courant d’obscurité ($d_\text{rate} \times t_{\text{lights}}$) mais qui ne dépend pas de la position du pixel sur le capteur. Et enfin il y a une valeur constante, l’offset. Ce décalage est présent dans n’importe laquelle des images, de sorte que nous le retrouvons dans toutes les expressions.
Les darks $D$ n’ayant pas été illuminés, ils n’ont que le terme de courant d’obscurité, de même intensité que les brutes car ils ont le même temps d’exposition, et le terme d’offset.
Les flats $F$ ont également un terme spatial, proportionnel au terme présent dans les brutes. Le facteur $K$, supérieur à 1, montre simplement que leur intensité est plus grande. Pour écrire cela, il suffit de supposer que les pixels répondent linéairement au nombre de photons qu’ils recoivent, ce qui est une hypothèse raisonnable. Nous aurions pu aussi écrire un terme de courant d’obscurité, proportionnel au temps de pose des flats. Mais à moins que le temps d’exposition ne soit significatif, nous pouvons supposer ce terme négligeable. Si ce n’est pas le cas, cela signifie que vous devez prendre des darkflats, ou au moins évaluer leur niveau.
Et enfin les offsets $O$ ne mesurent que le niveau de décalage au zéro.
Pour visualiser ces niveaux, j’ai tracé ci-dessous ces expressions sous forme de courbes en fonction de la position sur le capteur et je vous encourage à faire de même et à jouer avec les différentes valeurs.
- $a = 200 \text{[ADU]}$
- $b = 0.0003 \text{[ADU/px}^2\text{]}$
- $d_\text{rate} = 1 \text{[ADU/s]}$
- $t_{\text{lights}} = 10 \text{[s]}$
- $o = 2048 \text{[ADU]}$
- $W = 1000 \text{[px]}$
Les valeurs $L$, $D$ et $O$ en ADU sont données sur l’échelle de gauche tandis que l’expression $F$ est sur l’échelle de droite.
Maintenant, que signifie calibrer vos brutes? Lorsque vous calibrez vos brutes, vous effectuez l’opération suivante : $L_c = \dfrac{L -D}{F-O}$.
Le terme $F-O$ est un flat dont vous avez soustrait le niveau d’offset (qu’il s’agisse d’un offset maitre ou simplement d’un niveau, c’est-à-dire tout l’intérêt de ce tutoriel). Il s’agit de l’opération effectuée avant d’empiler votre flat maitre. Et le terme $L-D$ représente une brute dont vous avez soustrait le niveau de courant d’obscurité et l’offset, c’est-à-dire un dark maitre.
Si vous remplacez par les expressions ci-dessus, vous obtenez ce qui suit : $L_c = \dfrac{1}{K}$.
Aucun terme de variation spatiale ne reste, le niveau de fond de vos brutes est uniforme! Afin d’obtenir une valeur raisonnable en ADU (et non pas $1/K$), Siril choisit automatiquement un niveau lorsque vous cochez Auto évaluer la valeur de normalisation dans l’onglet Calibration.
Et vous pouvez essayer avec n’importe quelle autre combinaison, aucune autre ne se débarrassera des variations spatiales.
Pour illustrer cela, j’ai tracé ci-dessous le résultat de différentes combinaisons. Pour tout mettre sur la même échelle, tous les résultats sont normalisés pour avoir la même intensité de 1 au milieu du capteur. Les tests suivants sont présentés :
- $L-D$ : vous avez simplement pris des darks.
- $L/F$ : vous avez simplement pris des flats.
- $L/(F-O)$ : vous avez pris des flats et les avez corrigés par un offset (soit un offset maitre soit un synthétique).
- $(L-O)/(F-O)$ : vous avez pris des flats et les avez corrigés par un offset. Mais vous avez également soustrait cet offset de vos brutes.
- $(L-D)/F$ : Vous avez fait des darks et des flats mais pas d’offsets.
- $(L-D)/(F-O)$ : vous avez tout fait dans les règles de l’art.
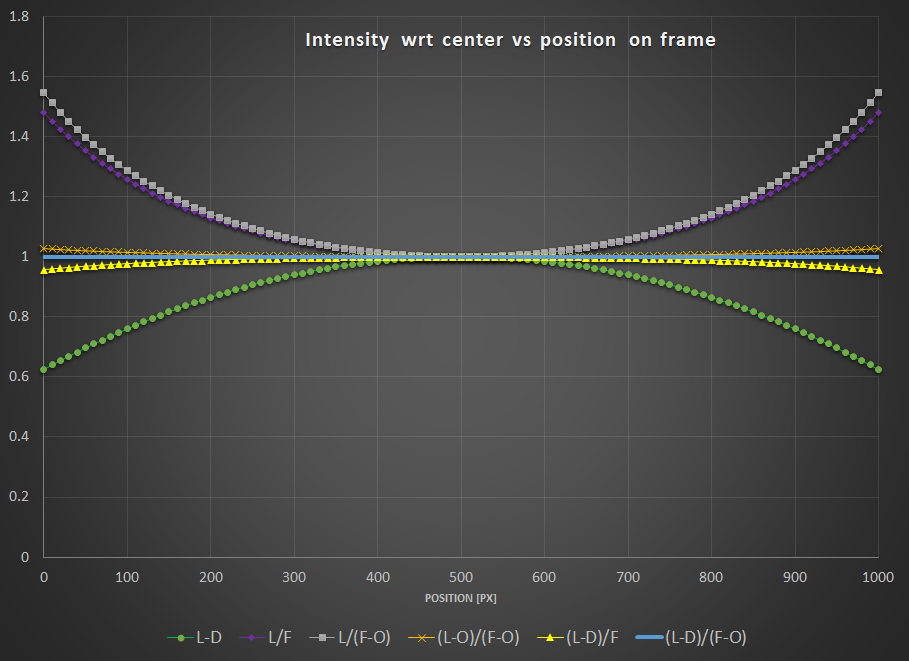
Vous pouvez remarquer que :
- $L-D$ ne montre évidemment aucune correction pour le vignettage.
- Les deux expressions $L/F$ et $L/(F-O)$ montrent une sur-correction ou vignettage inverse.
- Très proche du résultat optimal, $(L-D)/F$ et $(L-O)/(F-O)$ montre un champ quasi plat. Cela dépendra bien sûr de la quantité de courant d’obscurité de votre capteur ou du vignettage induit par votre optique.
- L’étalonnage de référence donne un champ complètement plat.
On peut donc en tirer les conclusions suivantes :
- Vous avez tout intérêt à corriger vos brutes avec un offset (un offset maitre ou simplement un niveau) si vous n’avez pas pris de darks.
- Mieux encore, si vous n’avez pas le temps de prendre une série de darks, cela vaut probablement la peine d’en prendre au moins un, de mesurer sa médiane et de soustraire ce niveau de dark (synthétique) de vos brutes. Cela ne corrigera bien sûr pas pour l’ampglow ou n’activera pas la correction des pixels chauds, mais le champ de vos brutes calibrées sera au moins plat!
Et quid des poussières…? Si vous voulez que les flats corrigent correctement vos brutes, il vous faudra malheureusement avoir fait tous les masters de calibration. Pour l’illustrer, ajoutons un petit déficit de lumière local sur les brutes et les flats.
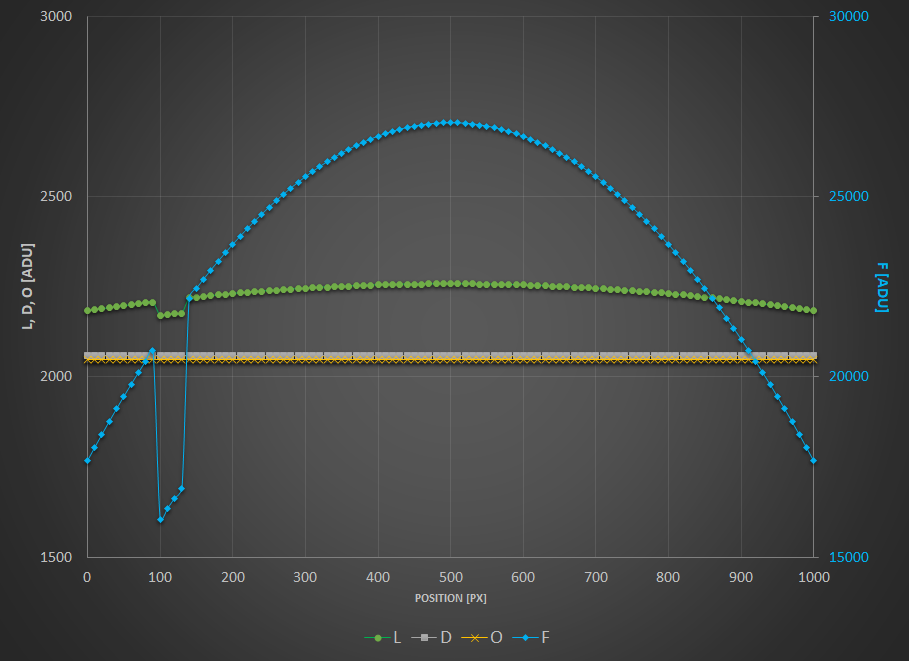
Comme vous pouvez le voir, seule la combinaison $(L-D)/(F-O)$ arrive a se débarasser de cette tache.
Pour illustrer plus avant les équations et les courbes ci-dessus, rien de mieux qu’un exemple réel. Toutes les photos reproduites ci-dessous sont utilisées avec l’aimable autorisation de G. Attard.

$L-D$

$L/F$

$L/(F-O)$

$(L-O)/(F-O)$

$(L-D)/(F-O)$