Rapport Signal sur Bruit
Signal et Bruit #
Habituellement, nous prenons plusieurs images avec un long temps d’exposition puis les empilons afin de réduire le bruit de l’ image de ciel profond. Nous faisons de longues poses parce que nous voulons obtenir plus de photons, afin d’augmenter notre signal. Nous empilons les images non pas pour ajouter leur lumière, mais pour faire la moyenne de leur bruit.
Lorsque nous détectons de la lumière, le nombre de photons que nous détectons n’est pas constant pour un niveau de luminosité fixe. Il fluctue aléatoirement autour d’un niveau moyen. Nous appelons cette fluctuation bruit de grenaille. Il est important de noter que ce bruit n’est pas introduit par l’équipement. Ce bruit de grenaille est proportionnel à la racine carrée du signal, donc un niveau de signal plus élevé a plus de bruit de grenaille que pour des niveaux inférieurs.
Ce bruit de grenaille est responsable des imperfections dans la suppression du signal des darks. Le signal des darks est causé par des photons thermiques provenant de l’environnement et de l’électronique de votre caméra. Ils exposent votre détecteur comme les vrais photons de la source lumineuse. Nous utilisons alors une opération de soustraction de d’image darks pour essayer de les supprimer. Lorsque vous empilez vos darks, vous calculez la moyenne du signal dark de chaque pixel à une valeur moyenne pour ce pixel. Mais dans chaque image brute, le signal dark est également affecté par son propre bruit de grenaille, de sorte que ce dernier n’éliminera jamais complètement le bruit produit par le signal dark.
Comme nous l’avons vu précédemment, le bruit est proportionnel à la $\sqrt{(\text{valeur})}$, donc le seul moyen de réduire son effet est de réduire le niveau du signal dark. À cette fin, nous utilisons généralement des caméras refroidies ou des temps d’exposition très courts. Les caméras refroidies ont moins de photons thermiques détectés par le détecteur. Les expositions courtes permettent à moins de photons d’atteindre chaque image, nous avons donc un signal dark plus faible qui est plus stable et plus facile à éliminer entièrement.
Imagerie Rapide #
Si vous avez un appareil photo refroidi, vous pouvez continuer à baisser la température et prendre de longues expositions pour capturer vos sujets. Mais si votre appareil photo n’est pas refroidi ou si son suivi n’est pas assez bon pour prendre de longues expositions, vous pouvez essayer de réduire le bruit en prenant de courtes expositions. Oui, je sais, cela semble contre-intuitif, mais pour certains types de caméra, cela fonctionne très bien. Ceci est lié à une autre source de bruit que j’ai ignorée jusqu’à présent, le bruit de lecture. Ce bruit est lié à la conversion des photons piégés sous forme d’électrons par le détecteur en un signal transféré vers votre ordinateur. De nombreux composants électroniques sont impliqués dans ce processus, mais il est caractérisé par un seul chiffre: le bruit de lecture, généralement exprimé en électrons / px.
Sur les caméras CCD classiques, ce bruit de lecture était d’environ 6 ou 7e / px. Et rappelez-vous que cette erreur est indépendante du signal, donc si votre exposition n’est pas assez longue pour accumuler plus de 7 électrons de signal, vous êtes désespérément coincé à cette étape à cause du bruit de lecture. C’est pourquoi, dans ce cas là, vous avez besoin de longues expositions pour détecter les sources faibles.
Aujourd’hui, les détecteurs les plus utilisés pour l’astrophotographie sont le CMOS et non le CCD. Ces détecteurs ont des conceptions d’électronique et de détecteur très différentes. Cela change beaucoup de choses. Celui qui nous intéresse ici est le bruit de lecture. Les caméras CMOS ont de très faibles niveaux de bruit de lecture. En fait, les caméras que nous utilisons pour la photographie planétaire ont tendance à avoir un bruit de lecture très proche ou inférieur à 1e / px.
À ce niveau de bruit de lecture, prendre des images 1x120s ou empiler des images 12x10s est presque identique, car le processus de lecture de chaque image individuelle n’ajoute pas une quantité significative de bruit. Vous pouvez voir une longue explication de l’auteur du logiciel SharpCap, le Dr Robin Glover, sur cet exposé (anglais)
Notre plan est donc de prendre des centaines ou des milliers d’images de courte exposition et de les empiler pour obtenir une image nette. Et cela fonctionne très bien ! En décembre dernier, j’ai utilisé une caméra QHY5III462C pour prendre 740x10s images de M1 avec un télescope de 85 mm et ensuite les empiler. Comme vous pouvez le voir, l’équivalent de 2 heures d’exposition me permet d’extraire beaucoup de détails fins :

Voir le signal émerger du bruit #
Le résultat final est bon, mais je veux voir comment cette image peut émerger de mes prises de vue de 10s. Parce que si je vous montre l’une d’entre elles, vous ne croirez PAS que ce résultat final provient de ces images individuelles. Examinons donc l’une d’entre elles, choisie au hasard:

Cette image a son histogramme déjà étiré, vous pouvez donc voir des étoiles, mais la nébuleuse est une tache amorphe au milieu de ce recadrage.
Une chose intéressante à propos de ce bruit de grenaille : notre système cerveau/œil sait comment le gérer. Partiellement. Chaque fois que vous voyez un film (vidéo), votre système cerveau/œil supprime ce bruit, de la même façon que les logiciels en empilant. C’est ce que nous appelons la persistance rétinienne . En gros, votre système visuel empile et fait la moyenne en continu de quelques fractions de seconde. Si vous êtes face à une courte rafale d’images individuelles, votre cerveau ne les voit pas une par une, mais comme une image composée. S’il y a des déplacements entre les images, vous voyez du mouvement.
Dans notre cas, si nous composons toutes les images brutes (étirées) sous forme de vidéo et les lisons à 24 ips, votre cerveau “moyenne” le bruit de grenaille et vous pouvez voir à travers le voile de bruit. Dans cette vidéo, vous pouvez voir comment les étoiles pâles apparaissent à travers la brume et comment la nébuleuse au milieu de l’image est mieux définie.

Donc, ce que je voulais, c’est voir comment l’image finale sort de cette mer de bruit et c’est là que les capacités de script de Siril entrent en jeu.
Mais avant de commencer le processus d’empilement, nous devons effectuer un traitement de base. Les étapes d’étalonnage et d’alignement seront les mêmes une fois de plus. Ainsi, la première phase de cette aventure sera d’exécuter le script OSC_Preprocess pour générer la séquence r_pp_light parfaitement calibrée et alignée, prête à être empilée. En fait, comme j’utilise une caméra couleur et que je ne peux pas équilibrer les couleurs de chaque image individuellement, j’ai choisi d’extraire le canal Halpha synthétique en utilisant le script OSC_Extract_Ha à la place. Cela produira un ensemble d’images monochromes. J’ai également utilisé l’interface graphique pour recadrer une sous-image de 1000x1000 centrée autour de la nébuleuse. Après les avoir renommés en org_xxxxx.fits, nous pouvons commencer par l’empilement.
Mon intention était de faire 740 empilements. Le premier n’est pas un empilement, mais une seule image. Le deuxième empilement ne contiendra que les images 1 et 2, le troisième empilement contiendra les images 1, 2 et 3 et ainsi de suite jusqu’à ce que nous atteignions l’empilement 740 qui contiendra toutes les images. Ce dernier sera la pile de l’empilement classique que nous effectuons dans une session habituelle, en empilant toutes les images.
De toute évidence, produire 740 empilements d’images à la main, avec des images différentes sur chacun, est une mission relativement décourageante. Alors j’ai commencé à penser aux scripts. Je sais que les scripts Siril sont limités - nous n’avons pas de variables, nous n’avons pas de déclarations de flux de contrôle. Mais Siril n’est pas seul. Dans une tradition pure Unix, Siril n’est pas seulement une application graphique sophistiquée où vous pouvez utiliser votre souris. C’est également un outil de ligne de commande qui peut être démarré pour exécuter une tâche et quitter. Et cette tâche pourrait être un script Siril.
Mon idée était donc d’utiliser des scripts bash pour coordonner l’ensemble du processus et faire le nettoyage et un script Siril très simple à empiler.
J’ai mis toutes les images empilées dans un dossier appelé anim. Ici, j’ai les images org_00001.fits, org_00002.fits … org_00739.fits. Nous allons itérer 739 fois et dans chaque boucle je copie une image dans un dossier appelé process. Ensuite, je démarre Siril avec un script personnalisé pour empiler les images dans le dossier process. Après que Siril ait produit sa sortie, je copie l’image empilée dans un nouveau dossier stacked avec le même nom que l’image nouvellement ajoutée. L’état initial est
À la fin du processus, j’aurai le dossier stacked rempli avec la séquence org_00001.fits, org_00002.fits … org_00739.fits, mais cette fois sur cette séquence, chaque image sera une pile incrémentielle.
Je vous montre d’abord le script Siril, et vous êtes déçu, car c’est très simple :
requires 0.99.4
cd process
stack org rej 3 3 -norm=addscale -output_norm
cd ..
Entrez dans le dossier process, empilez les fichiers org et sortez. Une tâche. Simple.
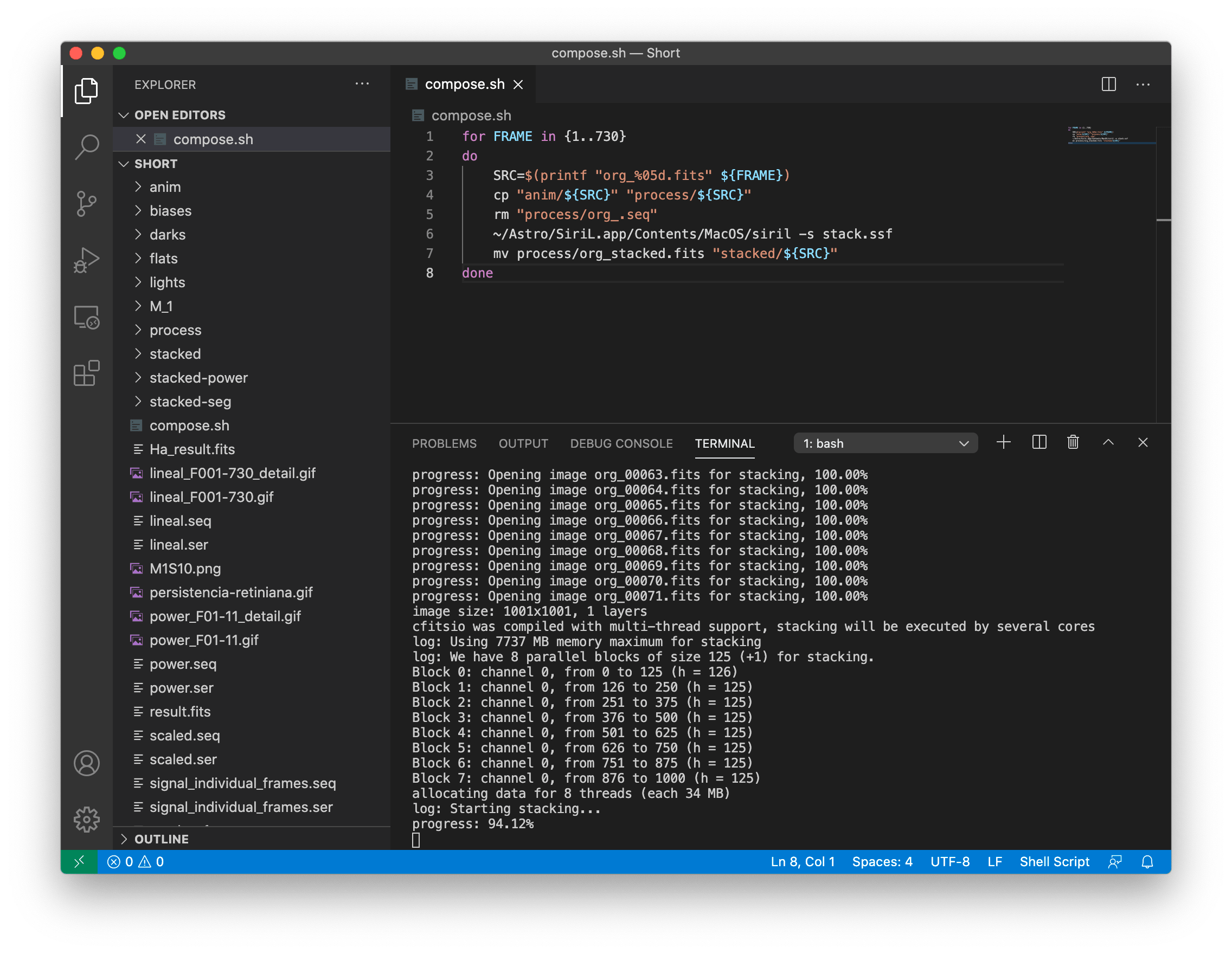
Ensuite, je vous montre le script bash qui exécute le tout :
for FRAME in {1..730}
do
SRC=$(printf "org_%05d.fits" ${FRAME})
cp "anim/${SRC}" "process/${SRC}"
rm "process/org_.seq"
~/Astro/SiriL.app/Contents/MacOS/siril-cli -s stack.ssf
mv process/org_stacked.fits "stacked/${SRC}"
done
Comme vous pouvez le voir, il n’y a rien de trop compliqué dans ce fichier non plus. Faîtes une itération sur le numéro de l’image, créez le nom du fichier d’image, copiez-le et lancez Siril. Une fois l’empilement terminé, enregistrez le fichier avec le nombre de l’image courante. Puisque j’exécute tout ce processus sur un ordinateur macOS, la façon dont je dois invoquer Siril est un peu étrange, mais à la fin, je lance juste Siril avec l’option -s et le nom du script.
Comme nous réutilisons le même dossier process à chaque exécution, il est important de supprimer le fichier .seq précédemment créé, sinon Siril ne verra pas la nouvelle image ajoutée.
Et c’est tout, exécutez ce script et prenez un café, car il faut un certain temps pour générer toutes les images de l’animation.
Sortir de la Mer de Bruit #
Une fois le processus terminé, j’ouvre l’interface graphique de Siril comme d’habitude, je sélectionne le dossier stacked comme dossier de travail, je recherche les séquences et transforme celle trouvée en fichier SER. Vous pouvez ouvrir cette vidéo dans SER Player pour voir l’image émergeant de la mer de bruit :). J’ai exporté la vidéo au format mp4 afin d’être visible sur cette page :
Comme vous pouvez le voir, l’image s’améliore image par image à mesure que vous ajoutez plus de composants à la pile. Non seulement le contraste augmente et le niveau de bruit de fond diminue, mais vous pouvez voir des détails fins émerger dans la nébuleuse alors que le bruit de grenaille est de plus en plus moyenné.
Au début, les améliorations sont nettement plus apparentes, puis le taux d’amélioration commence à ralentir. Vous vous demandez peut-être combien d’images devez-vous empiler?
Autant que vous le pouvez. Le rapport signal sur bruit s’améliore toujours lorsque vous ajoutez plus d’images. Le problème est que le rapport des améliorations n’est pas linéaire avec le nombre d’images empilées.
En général, le rapport signal sur bruit pour les empilements dépend de la $\sqrt{(\text{N})}$ où N est le nombre d’images empilées. Si vous regardez le graphique de la $\sqrt{(\text{N})}$, vous verrez que la pente devient moins prononcée à mesure que N augmente, de sorte que le nombre d’images que vous devez ajouter augmente avec le nombre d’images déjà empilées.
Par exemple, j’ai extrait la pile intitulée 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 et 730 (ce dernier devrait être1024, mais je n’ai pas assez d’images !). Chaque pile a deux fois plus d’images que la précédente. Donc, si nous regardons le rapport signal sur bruit, nous trouvons que le rapport pour la pile de N-images est
$$
N_i = 2N_{i - 1}
$$
$$
\sqrt{N_i} = \sqrt{2N_{i-1}} = \sqrt{2}\sqrt{N_{i-1}}
$$
$$
\text{SNR(Stack)}_i=1.41\times \text{SNR(Stack)}_{i-1}
$$
Ainsi, dans cette séquence, chaque image a un rapport signal sur bruit 1,41 fois meilleur que la précédente. Nous espérons voir une amélioration constante de la qualité d’image. Et en fait c’est ce que vous pouvez voir dans les animations suivantes.

Conclusion #
Siril n’est pas seulement un bel outil pour produire des images époustouflantes. Il peut également être un outil utile qui s’intègre dans des chaînes d’outils plus larges de plusieurs autres outils.
Et rappelez-vous que si vous avez des images N et que vous souhaitez améliorer considérablement la qualité, ne pensez pas à ajouter des images, pensez à doubler le nombre.